Teoretisk beregning af mundingshastigheden

Beregninger på kartoffelkanonen involverer en del fysiske begreber, som vi vil gennemgå i det følgende.

Kartoffelkanonen virker ved, at komprimeret luft fremdriver et projektil. Den komprimerede luft befinder sig i en trykbeholder med volumen $V_0$.

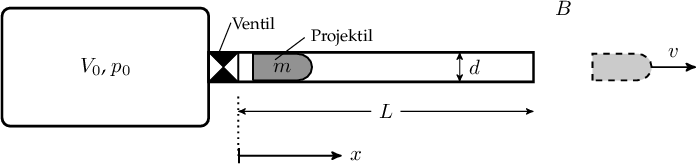
Vi betegner starttrykket i beholderen for $p_{0}$ og barometertrykket for $B$.

(Det tryk, som vi aflæser på trykluftspistolens manometer er overtrykket $p_{0} - B$. Altså er trykket i beholderen altid cirka 1 bar større end manometeraflæsningen på pistolen).

Da trykket på den ene side af projektilet er større end trykket på den anden side af projektilet, giver det anledning til en kraft, som tvinger projektilet ud af røret. Så snart projektilet er ude af røret, vil der ske en trykudligning, således at fremdriften stopper. På dette tidspunkt har projektilet hastigheden $v$.

Tryk er defineret ved

$$p = \frac{F}{A}$$

hvorved

$$F = p \cdot A$$

Her er $A$ rørets tværsnitsareal.

Vi kan nu lave et kraftdiagram på projektilet.

Friktionskraften mellem projektilet og røret betegner vi $F_{\mu}$. Kraften fra luften i beholderen er $F$ og kraften fra den atmosfæriske luft i rørets åbne ende er $F_{\text{atm}}$.

Mens

$$F_{\text{atm}} = A \cdot B$$

er konstant, så aftager trykkraften

$$F = A \cdot p$$

ud gennem røret, da trykket $p$ i beholderen aftager med rørets længde $x$.

Newtons 2. lov giver os

\begin{equation} m \cdot a = F - F_{\text{atm}} - F_{\mu} \end{equation}

eller på differentiel form

$$m \cdot \frac{\mathrm{d}v}{\mathrm{d}t} = A \cdot p - A \cdot B - F_{\mu}$$

Nu er

$$\frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}x}{\mathrm{d}x} \cdot \frac{\mathrm{d}v}{\mathrm{d}t} = \frac{\mathrm{d}x}{\mathrm{d}t} \cdot \frac{\mathrm{d}v}{\mathrm{d}x} = v \cdot \frac{\mathrm{d}v}{\mathrm{d}x}$$

så vi kan udtrykke (1) som

\begin{equation}m \cdot v \cdot \frac{\mathrm{d}v}{\mathrm{d}x} = A \cdot p - A \cdot B - F_{\mu}\end{equation}

Denne differentialligning kan vi løse, hvis vi kan udtrykke trykket $p$ som funktion af $x$.

Når vi åbner for ventilen, vil luften i beholderen ekspandere.

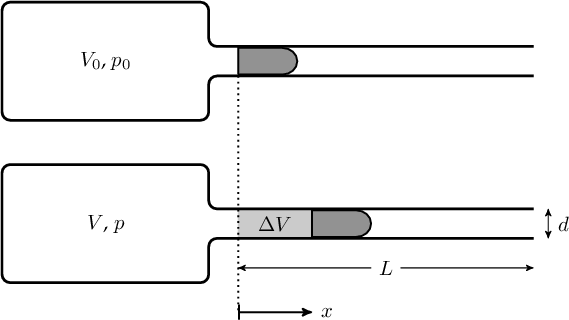
Antager vi, at luften ekspanderer så hurtigt, at det sker uden varmeudveksling med omgivelserne (kanonen og projektilet), kan vi benytte formlen for en adiabatisk ekspansion af en ideal gas

$$p_0 \cdot V_0^{\gamma} = p \cdot V^{\gamma} \,\,\,\,\,\,\,\,\, \text{, for luft er } \gamma = 1,4$$

Vi har altså

\begin{equation}p = p_0 \cdot \left(\frac{V_0}{V}\right)^{\gamma}\end{equation}

Af figuren fremgår, at $V = V_0 + \Delta V$, hvor $\Delta V$ er det øgede volumen af luften i beholderen, og da

$$\Delta V = A \cdot x$$

kan vi udtrykke (3) som

$$p = p_0 \cdot \left(\frac{V_0}{V_0 + A \cdot x}\right)^{\gamma}$$

Da vi nu har udtrykt $p$ som funktion af $x$, kan vi indsætte dette udtryk i (2). Så får vi

$$m \cdot v \cdot \frac{\mathrm{d}v}{\mathrm{d}x} = A \cdot p_0 \cdot \left(\frac{V_0}{V_0 + A \cdot x}\right)^{\gamma} - A \cdot B - F_{\mu}$$

Ved separation af de variable får vi med lidt omskrivning

$$m \cdot \int \!v \, \mathrm{d}v = \int \left( A \cdot p_0 \cdot V_0^{\gamma} \cdot \left( V_0 + A \cdot x \right)^{- \gamma} - A \cdot B - F_{\mu} \right) \, \mathrm{d}x$$

Nu integrerer vi over hele rørets længde

$$ m \cdot \int\limits_{0}^{v_{\text{slut}}} \!v \, \mathrm{d}v = \int\limits_{0}^{L} \left( A \cdot p_0 \cdot V_0^{\gamma} \cdot \left( V_0 + A \cdot x \right)^{- \gamma} - A \cdot B - F_{\mu} \right) \, \mathrm{d}x$$

altså

\begin{equation}m \cdot \int\limits_{0}^{v_{\text{slut}}} \!v \, \mathrm{d}v = A \cdot p_0 \cdot V_0^{\gamma} \cdot \int\limits_{0}^{L} \left( V_0 + A \cdot x \right)^{- \gamma} \, \mathrm{d}x - \int\limits_{0}^{L} A \cdot B \, \mathrm{d}x - \int\limits_{0}^{L} F_{\mu} \, \mathrm{d}x \end{equation}

Fra matematik er det velkendt, at

$$\int \!(ax+b)^n \, \mathrm{d}x = \frac{(ax+b)^{n+1}}{(n+1) \cdot a}$$

så ved integration af (4) får vi

$$\frac{1}{2} \cdot m \cdot v_{\text{slut}}^2 = A \cdot p_0 \cdot V_0^{\gamma} \cdot \bigg[ \frac{(V_0+A \cdot x)^{-\gamma +1}}{(- \gamma +1) \cdot A} \bigg]_{0}^{L} -A \cdot B \cdot L - F_{\mu} \cdot L$$

og dermed

$$\frac{1}{2} \cdot m \cdot v_{\text{slut}}^2 = A \cdot p_0 \cdot V_0^{\gamma} \cdot \left( \frac{(V_0+A \cdot L)^{1-\gamma}}{(1- \gamma) \cdot A} - \frac{V_0^{1-\gamma}}{(1-\gamma) \cdot A}\right) -A \cdot B \cdot L - F_{\mu} \cdot L$$

eller

$$\frac{1}{2} \cdot m \cdot v_{\text{slut}}^2 = \frac {\cancel{A} \cdot p_0 \cdot V_0^{\gamma}}{(1- \gamma) \cdot \cancel{A}} \cdot \left( (V_0+A \cdot L)^{1-\gamma} - V_0^{1-\gamma} \right) -A \cdot B \cdot L - F_{\mu} \cdot L$$

Vi udnytter nu, at $1 - \gamma = - (\gamma - 1)$, og at $V_0^{\gamma} = V_0 \cdot V_0^{\gamma - 1}$. Så får vi

$$\frac{1}{2} \cdot m \cdot v_{\text{slut}}^2 = \frac {p_0 \cdot V_0 \cdot V_0^{\gamma-1}}{-(\gamma-1)} \cdot \left( \left( \frac{1}{V_0+A \cdot L}\right)^{\gamma-1} - \left( \frac{1}{V_0}\right)^{\gamma-1} \right) -A \cdot B \cdot L - F_{\mu} \cdot L$$

og igen

$$\frac{1}{2} \cdot m \cdot v_{\text{slut}}^2 = \frac {p_0 \cdot V_0}{\gamma-1} \cdot \left(1 - \left( \frac{V_0}{V_0+A \cdot L}\right)^{\gamma-1} \right) -A \cdot B \cdot L - F_{\mu} \cdot L$$

Endelig får vi det ønskede udtryk for mundingshastigheden

\begin{equation} \underline{v_{\text{slut}} = \sqrt{\frac{2}{m}} \cdot \sqrt{\frac {p_0 \cdot V_0}{\gamma-1} \cdot \left(1 - \left( \frac{V_0}{V_0+A \cdot L}\right)^{\gamma-1} \right) -A \cdot B \cdot L - F_{\mu} \cdot L}}\end{equation}

I praksis er friktionskraften meget lille i forhold til trykkraften, så den kan man tillade sig at negligere.

 

Beregningseksempel

Vi kan nu indsætte værdier for kartoffelkanonen i ovenstående udtryk for mundingshastigheden.

Beholderens indvendige diameter er 57 mm og den samlede rørlængde er 3 m. Så beholderens volumen er

$$V_0 = \frac{\pi}{4} \cdot (0,057\,m)^2 \cdot 3\, m = \underline{0,0077 \,m^3} = 7,7 \, L$$

Kanonrørets indvendige diameter er $d = 45 \, mm$ og dets længde er $L = 1,8 \, m$. Så kanonrørets volumen er

$$A \cdot L = \frac{\pi}{4} \cdot (0,045\,m)^2 \cdot 1,8\, m = \underline{0,0029 \,m^3} = 2,9 \, L$$

Som tidligere nævnt er $\underline{\gamma = 1,4}$ for luft.

En typisk værdi for massen af et kartoffelprojektil er $\underline{m = 80 \, \text{g}}$.

Barometertrykket er som standard $B = 1 \, \text{atm} = 1,01 \, \text{bar} = \underline{101.000 \, \text{Pa}}$.

Ladetrykket (manometervisningen) sætter vi til 5,0 bar, hvorved starttrykket i beholderen er

$$p_0 = 5,0 \, \text{bar} + B = 5,0 \, \text{bar} + 1,01 \, \text{bar} = 6,01 \, \text{bar} = \underline{601.000 \, \text{Pa}}$$

Ignorerer vi friktionskraften mellem projektil og kanonrør, får vi ved indsættelse i det teoretiske udtryk (5)

\begin{align*} v_{\text{slut}} &= \scriptsize \sqrt{\frac{2}{0.080\,\text{kg}}} \cdot \sqrt{\frac {601.000\,\text{Pa} \cdot 0,0077\,\text{m}^3}{0,4} \cdot \left(1 - \left( \frac{0,0077\,\text{m}^3}{0,0077\,\text{m}^3+0,0029\,\text{m}^3}\right)^{0,4} \right) -0,0029\,\text{m}^3 \cdot 101.000\,\text{Pa}} \\ &= \underline{166\,\text{m/s}}\end{align*}

Denne værdi for mundingshastigheden er den teoretisk maksimale værdi og tager ikke hensyn til, at det i praksis er umuligt at åbne ventilen øjeblikkeligt. Den teoretiske formel tager heller ikke højde for, at ventilhullets diameter er mindre end kanonrørets diameter, hvilket gør, at trykket i røret er mindre end trykket i beholderen (dysevirkning).

Kartoffelprojektilet slutter heller ikke helt tæt til kanonrøret, hvilket betyder, at noget af luften presser sig forbi kartoflen, se billedserien herunder.